통신으로 전달되는 암호문은 누구나 접근가능하기 때문에, 해독 및 변조를 어렵게 암호화 해야한다.
암호화 방식 중 대칭키 암호(Symmetric Key Encryption), 공개키 암호(Asymmetric Key Encryption, Public Key Encryption)이 대표적인데, 이 둘은 암호화와 복호화키의 동일함의 여부에 차이를 갖는다.
사전키 공유방식을 한계로 갖는 대칭키 암호화 방식에는 DES, AES이 해당하고, 복잡한 연산량으로 인한 속도저하를 단점으로 갖는 공개키 암호화 방식에는 RSA, EIGamal이 해당한다.
이번 글에서는 AES와 RSA에 대해 자세히 알아보자.
1. AES(Advanced Encryption Standard)-대칭키 암호화 방식
원래 대칭키 암호화 방식으로 사용되던 DES알고리즘에서 취약점이 발견되었고, 이를 대체하기 위해 AES가 등장하여 현재 전 세계적으로 사용되고 있다. feistel 구조를 갖고있는 DES와 달리 AES는 SPN구조를 갖고 있어서 병렬처리에 용이하다. 128비트씩의 평문을 암호화하는 것이라고 생각하면 되고(128비트의 블럭에서 계속 계산하여 암호화한다고 생각하면 된다. 블럭 하나당 8비트에 해당하기 때문에 이는 계산할 때에도 고려된다.), 대체로 4*4형태로 배열한 후에 계산한다. 키길이의 bit수에 따라 라운드 수가 달라지는데, 128비트의 키를 사용한다면 10번의 라운드, 192비트의 키를 사용한다면 12번의 라운드, 256비트의 키를 사용한다면 14번의 라운드의 암호화 과정을 수행해야한다.
128비트에서 256비트 사이의 키를 적용할 수 있어 보안성 뛰어나며, 공개된 알고리즘이라 누구나 사용가능하다.
암호화과정 - 첫번째 라운드, 메인 라운드, 마지막 라운드를 순서대로 수행
(본 글에서는 128비트의 경우를 다뤄보자)
첫번째 라운드에서 암호화하고자 하는 128비트의 데이터에 라운드 키를 더하고(XOR연산), 메인라운드에서 SubBytes, ShiftRows, MixColumns를 거친 뒤 또다시 라운드 키를 더하는 과정을 9번 반복하고, 마지막 라운드에서는 SubBytes, ShiftRows만을 거친 뒤에 라운드키를 더해서 암호화한다. 평문과 라운드키, 최종적인 암호문의 크기는 동일하다.
첫번째 라운드 :
AddRoundkey
메인 라운드(encryption round) : 9번 반복한다.
SubBytes (모든 값을 변환해주고)
ShiftRows (4*4로 배열한 암호문을 가로로 섞어주고)
MixColumns (4*4로 배열한 암호문을 세로로 섞어주고)
AddRoundKey (계속 바꿔주는 키로 XOR연산해주고)
해당 암호화 키길이의 bit수에 따라 (라운드수-1)번만큼 2를 반복한다.
(키길이의 bit수에 따라 라운드 수가 달라지는데, 128bit 경우에는 라운드 수가 10번으로, 192bit는 12로, 256bit는 14로 정해진다.)
마지막 라운드
SubBytes
ShiftRows
AddRoundKey
마지막 라운드는 MixColumns를 제외하고 수행한다.
라운드에서 수행되는 변환과정(SubBytes, ShiftRows, MixColumns, AddRoundKey)
SubBytes :
AES 연산이 수행되는 GF(2^8)에서 1 바이트의 역원을 구한 후(확장된 유클리드 호제법으로 구할 수 있다) 아핀변환을 해준다. 8비트씩 연산해주어 128비트를 모두 치환해주는 것인데, 변환이 일어나는 모든 경우를 미리 구해놓은 S-BOX를 이용하여 치환할 수도 있다.
(S-BOX는 substitution box의 약자인데, AES알고리즘의 보안성을 증가시켜주는 요인이 된다.)
S-BOX에는 각각의 hex값에 대응되는 값이 있는데, 이를 이용해서 모든 hex값을 대응되는 값으로 변환해준다.
ShiftRows :
행 단위로 shift 연산을 해주는데, 2행은 1바이트씩 왼쪽으로 shift해주고, 3행은 2바이트씩, 4행은 3바이트씩 shift 해준다.
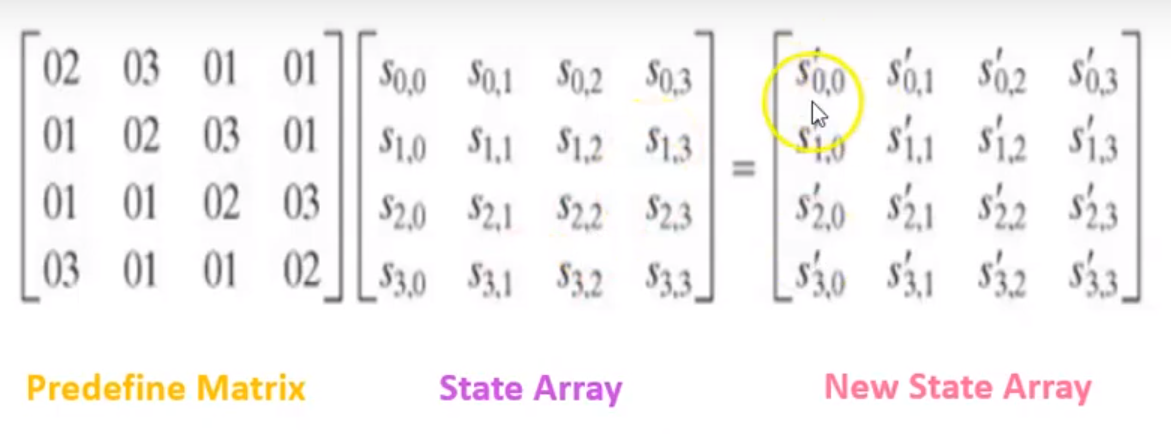
MixColumns :
각각의 column(열)별로 암호화에 쓰이는 행렬과 곱연산해주어 변환해준다. 첫번째, 두번째, 세번째, 네번째 열 모두 동일하게 행렬의 곱으로 변환해주면 된다.
이때 곱셈해주고 XOR연산해주기 전의 결과값이 256이상의 수라면 캐리가 발생하게 되기 때문에(한 칸에 255까지의 수만 담길 수 있다) , XOR 전에 256을 빼주어야한다.
[그림들 문제 푼 후에 지울 예정]

이런식으로 코드를 구현해보고자 한다.

AddRoundKey :
평문과 암호화키를 XOR연산해준다.
2. RSA(Rivest-Shamir-Adleman : 알고리즘 공개한 사람들 이름)-공개키 암호화 방식
RSA는 가장 많이 사용되고 있는 공개키 암호 시스템으로 1977년 공개된 이후 지금까지 사용되고 있는데, 현재의 사용 예시로는 SSL 보안 서버의 암호화인증서, pgp, 전자서명 등이 있다. 하지만 대칭키 암호화방식인 AES에 비해 속도가 느리기 때문에 메세지 암호화보다는 키암호화에 주로 쓰인다.
공개키 암호화 방식에서의 핵심인 공개키로부터 개인키 추측이 어렵게 하는 것을 위해 큰 숫자가 갖는 소인수분해의 어려움을 이용한다.
공개키 암호시스템이지만 개인키로 암호화하고 공개키로 복호화하는 것도 가능하다고 한다.
암호화과정 - 공개키, 개인키 생성 후 계산
공개키, 개인키 생성
1. 서로 다른 소수 p와 q 선택
(p와 q의 크기가 작을수록 인수분해가 쉬워지기 때문에 충분한 크기로 선택해야 한다.)
2. N=pq으로 N을 구함
(이때, pq에서 N을 구하는건 쉽지만, 반대로 N에서 pq를 구하는 것은 어렵다는 것을 이용한 키 생성 방법이다.)
3. 오일러파이함수로 N보다 작은 자연수 중 N과 서로소인 자연수의 개수를 구함
4. 오일러파이함수로 구한 값보다 작으면서 그 값과 서로소인 자연수를 e로 선택한다.
->ed=1mod(p-1)(q-1)가 되어 개인키인 d 값을 구할 수 있다.
이 때의 공개키는 (N, e)이다.
* 공개키 e는 2^16 + 1 = 65537 이나 이와 가까운 값을 사용할 것이 권고된다.
암호화
암호화 주체가 해독할 주체의 공개키를 알고 있기 때문에(N, e) 아래와 같이 암호화할 수 있다.
c=m^e
(c:암호문, m:평문, e:공개키)
※모듈로 연산(mod 연산)을 해주어야 한다
복호화
암호화된 메세지 c를 받은 복화화 주체는 N과 d를 알고있기 때문에 아래의 공식을 통해 평문으로 복호화할 수 있다.
m=c^d
(m:평문, c:암호문, d:개인키)
※모듈로 연산(mod 연산)을 해주어야 한다
암호의 목표 중 하나(부인방지)의 기능을 제공하기 때문에 광범위하게 사용되고 있지만, 양자 컴퓨터의 실용화가 이루어지면 RSA알고리즘은 무용해질 것이란 전망이 있다.
RSA에의 공격방식
오랫동안 다양하게 사용되어오다 보니 다양한 공격방식들이 암호학자들에 의해 제시되었다.
1. 메세지 크기가 작은 경우
2. e가 작은 경우
e가 작을수록 암호화에 드는 시간이 적어지기 때문에, e가 작은 경우에 가능한 다양한 공격이 존재한다. (위에서 언급했듯이, 작은 e를 사용할 때의 공격을 막기 위해 e는 65537로 정하는 경우가 많다.)
e로 사용될 수 있는 가장 작은 값은 3이다.
RSA문제를 풀 떄는
d값 계산, 낮은 지수 공격, n값 소인수 분해 및 DB이용, 위너공격, 하스타드 공격, 선택적 암호문 공격, p와 q값이 비슷할 경우 n값으로 p와 q값 구하기 등이 있다.
e값 클 때는 위너공격을, e값이 작을 때는 하스타드 공격을 사용할 수 있다.
추가내용
공개키 암호화방식에서도 키생성 방식의 차이로 암호해독 방식이 '소인수분해 문제와 이산대수 문제' 2갈래로 나누어진다. 대표적으로 본문 초반에 언급한 RSA는 소인수분해 문제로 접근해야하고, EIGamal는 이산대수 문제로 접근해야한다.
'스터디 > 암호학' 카테고리의 다른 글
| tcp (0) | 2020.09.29 |
|---|---|
| 암호학 문제 (0) | 2020.09.25 |
| 간단한 암호 문제 풀이 (0) | 2020.09.15 |


